Mathematical cognition and sets a la Lakoff & Nunez: Part II, the cognition of sets
Where I try to explain this stuff and hopefully don't completely screw it up.
In the preface to their book, Lakoff & Nunez have this to say about how our ideas are shaped.
So, what are the conceptual metaphors and how are they grounded? This is, I hope, a simple explanation. Let’s start with image schemas. Think of a schema as a kind of script or guide for understanding how the world works, how you interact with the world. An image schema is used to describe and understand spatial relationships. They are apparently universal conceptual primitives.2 The particular image schema of importance to the understanding of sets is that of the container schema.
The following is provided as an example, with an illustration that includes Venn diagrams (remember those?), of the built in spatial logic of the container schema.
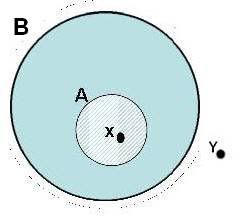 1. Given two Container schemas A and B and an object X, if A is in B and X is in A, then X is in B.
1. Given two Container schemas A and B and an object X, if A is in B and X is in A, then X is in B.
2. Given two Container schemas A and B and an object Y, if A is in B and Y is outside of B, then Y is outside of A.
When you look at the Venn diagram that illustrates these two statements, the spatial logic should be obvious and the schemas, with their built-in logics, can function as the concept and these schemas can also be used directly when reasoning about the concept. In theory, you can replace the various mathematical symbols that indicate membership in a set with this container image schema.5
Lakoff & Nunez continue with a description of the roles of various neural circuitry in generating these image schema before returning to the idea of containment.
This should lead to the metaphorical concept of a set as first a collection and then projecting the container metaphor onto the numerical collection. But a further metaphor is needed. One that allows us to look at how sets are defined as classes within the container metaphor and one that allows us to understand the set axioms within this framework.
Let’s back-up a few steps and look at the idea of conflation. Conflation is the simultaneous activation of two brain regions – two kinds of experiences – which when activated at the same time produce a single complex experience (i.e., affection as warmth). Conceptual metaphor creates a cross-domain mapping that explains this experience and preserves the structure of image schema. In terms of sets, what is and how does this cross-domain mapping occur? Begin with the spatial inference – container – and map this to an abstract idea – category. The mapping occurs in this manner. (Note that mappings are unidirectional. You go from the concrete to the abstract.)9
Categories are Containers
You can further delineate and map the container concept to the abstract concept of class. The mapping, shown below, brings us closer to an understanding of the metaphor/image-schema and underlying cognitive process that provides the understanding and manipulation of the abstract notion of sets. Starting with the container schema and its representation as a bounded region of space, move to the intuition that something is either inside or outside of this region. You now have a metaphorical concept of class where something inside the container belongs to the class while something outside the container does not. Through a metaphorical mapping, a grounding metaphor of Classes as Containers arises.10
Classes are Containers
Lakoff & Nunez observe that the Zermelo-Fraenkel axioms with the Axiom of Choice do not characterize sets as containers. Sets and membership within sets are undefined primitives. However, they argue that most of us conceptualize sets in terms of a container schema and that this conceptualization is consistent with the axioms. In addition, the Venn diagrams used when first learning set theory explicitly make use of the container schema. Lakoff & Nunez also point out that the use of the container schema removes the paradox addressed by the Axiom of Choice. If a set is conceived of as a container, a set can not be a member of itself since it is nonsensical to conceptualize a container as being inside itself.11
All references are to: Lakoff, G. & Nunez, R.E. (2000). Where mathematics comes from: How the embodied mind brings mathematics into being. Basic Books: New York: NY
1p. xiv
2p. 30
3pp. 30-31
4p. 31
5p. 31-33
6p. 33
7p. 53
8p. 54
9p. 43
10p.122-123
11p. 145
In the preface to their book, Lakoff & Nunez have this to say about how our ideas are shaped.
One of the great findings of cognitive science is that our ideas are shaped by our bodily experiences – not in any simpleminded one-to-one way but indirectly, through the grounding of our entire conceptual system in everyday life. The cognitive perspective forces us to ask, is the system of mathematical ideas also grounded indirectly in bodily experiences? And if so, exactly how?1Their explanation of how we conceptualize and handle mathematical sets is placed within this idea with the necessary grounding of the concepts rooted in conceptual metaphors. You’re probably thinking of metaphor as you learned it in high school English. This is similar, but different. These metaphors are part of your unconscious cognitive structure – you are unaware of them, but they structure how you think and relate to the world.
So, what are the conceptual metaphors and how are they grounded? This is, I hope, a simple explanation. Let’s start with image schemas. Think of a schema as a kind of script or guide for understanding how the world works, how you interact with the world. An image schema is used to describe and understand spatial relationships. They are apparently universal conceptual primitives.2 The particular image schema of importance to the understanding of sets is that of the container schema.
The Container schema has three parts: an Interior, a Boundary, and an Exterior. This structure forms a gestalt, in the sense that the parts make no sense without the whole…This structure is topological in the sense that the boundary can be made larger, smaller, or distorted and still remain the boundary of a Container schema.3Lakoff & Nunez further state that image schema have a special cognitive function in that they are both perceptual and conceptual, thus providing a bridge between our language and reasoning and our vision and visual/spatial perceptions. You can see milk as in the glass (with glass as the container) or bees in the garden (where the garden is a non-physical container). Lakoff & Nunez further note that this type of image schema has a built in spatial logic because of its image-schematic structure.4
The following is provided as an example, with an illustration that includes Venn diagrams (remember those?), of the built in spatial logic of the container schema.
 1. Given two Container schemas A and B and an object X, if A is in B and X is in A, then X is in B.
1. Given two Container schemas A and B and an object X, if A is in B and X is in A, then X is in B.2. Given two Container schemas A and B and an object Y, if A is in B and Y is outside of B, then Y is outside of A.
When you look at the Venn diagram that illustrates these two statements, the spatial logic should be obvious and the schemas, with their built-in logics, can function as the concept and these schemas can also be used directly when reasoning about the concept. In theory, you can replace the various mathematical symbols that indicate membership in a set with this container image schema.5
Lakoff & Nunez continue with a description of the roles of various neural circuitry in generating these image schema before returning to the idea of containment.
The concept of containment is central to much of mathematics. Closed sets of points are conceptualized as containers, as are bounded intervals, geometric figures, and so on. The concept of orientation is equally central…The concepts of containment and orientation are not special to mathematics but are used in thought and language generally. Like any other concepts, these arise only via neural mechanisms in the right kind of neural circuitry. It is of special interest that the neural circuitry we have evolved for other purposes is an inherent part of mathematics, which suggests that embodied mathematics does not exist independently of other embodied concepts used in everyday life. Instead, mathematics makes use of our adaptive capacities – our ability to adapt other cognitive mechanisms for mathematical purposes.6Now let’s take a look at the metaphorical constructs Lakoff & Nunez use when talking about mathematics in general and sets in particular. These constructs come in two flavors: grounding metaphors and linking metaphors. Although both are defined below, only the grounding metaphor will be used here when describing the cognitive/conceptual ideas underlying sets.
Grounding metaphors yield basic, directly grounded ideas. Examples: addition as adding objects to a collection, subtraction as taking objects away from a collection, sets as containers, members of a set as objects in a container. These usually require little instruction.These metaphors preserve inferences and ground the understanding of mathematics in prior understandings of every day physical activities. A primary method for metaphor to preserve these inferences is through the image-schema structure. The example given is that of forming a collection or pile of objects and then conceptualizing that collection as a container – “that is a bounded region of space with an interior, an exterior, and a boundary – either physical or imagined.” Lakoff & Nunez suggest that when numbers are conceptualized as collections, the logic of collections is projected onto the numbers.8
Linking metaphors yield sophisticated ideas, sometimes called abstract ideas. Examples: numbers as points on a line, geometrical figures as algebraic equations, operations on classes as algebraic operations. These require a significant amount of explanation.7
This should lead to the metaphorical concept of a set as first a collection and then projecting the container metaphor onto the numerical collection. But a further metaphor is needed. One that allows us to look at how sets are defined as classes within the container metaphor and one that allows us to understand the set axioms within this framework.
Let’s back-up a few steps and look at the idea of conflation. Conflation is the simultaneous activation of two brain regions – two kinds of experiences – which when activated at the same time produce a single complex experience (i.e., affection as warmth). Conceptual metaphor creates a cross-domain mapping that explains this experience and preserves the structure of image schema. In terms of sets, what is and how does this cross-domain mapping occur? Begin with the spatial inference – container – and map this to an abstract idea – category. The mapping occurs in this manner. (Note that mappings are unidirectional. You go from the concrete to the abstract.)9
| Source Domain: Containers | --> | Target Domain: Categories |
| Bounded regions in space | --> | Categories |
| Objects inside the bounded regions | --> | Category members |
| One bounded region inside another | --> | A subcategory of a larger category |
You can further delineate and map the container concept to the abstract concept of class. The mapping, shown below, brings us closer to an understanding of the metaphor/image-schema and underlying cognitive process that provides the understanding and manipulation of the abstract notion of sets. Starting with the container schema and its representation as a bounded region of space, move to the intuition that something is either inside or outside of this region. You now have a metaphorical concept of class where something inside the container belongs to the class while something outside the container does not. Through a metaphorical mapping, a grounding metaphor of Classes as Containers arises.10
| Source Domain: Container Schemas | --> | Target Domain: Classes |
| Interiors of Container schemas | --> | Classes |
| Objects as interiors | --> | Class members |
| Being an object in an interior | --> | The membership relation |
| An interior of one Container schema within a larger one | --> | A subclass in a larger class |
| The overlap of the interiors of two Container schema | --> | The intersection of two classes |
| The totality of the interiors of two Container schema | --> | The union of two classes |
| The exterior of a Container schema | --> | The compliment of a class |
Lakoff & Nunez observe that the Zermelo-Fraenkel axioms with the Axiom of Choice do not characterize sets as containers. Sets and membership within sets are undefined primitives. However, they argue that most of us conceptualize sets in terms of a container schema and that this conceptualization is consistent with the axioms. In addition, the Venn diagrams used when first learning set theory explicitly make use of the container schema. Lakoff & Nunez also point out that the use of the container schema removes the paradox addressed by the Axiom of Choice. If a set is conceived of as a container, a set can not be a member of itself since it is nonsensical to conceptualize a container as being inside itself.11
All references are to: Lakoff, G. & Nunez, R.E. (2000). Where mathematics comes from: How the embodied mind brings mathematics into being. Basic Books: New York: NY
1p. xiv
2p. 30
3pp. 30-31
4p. 31
5p. 31-33
6p. 33
7p. 53
8p. 54
9p. 43
10p.122-123
11p. 145


0 Comments:
Post a Comment
<< Home